
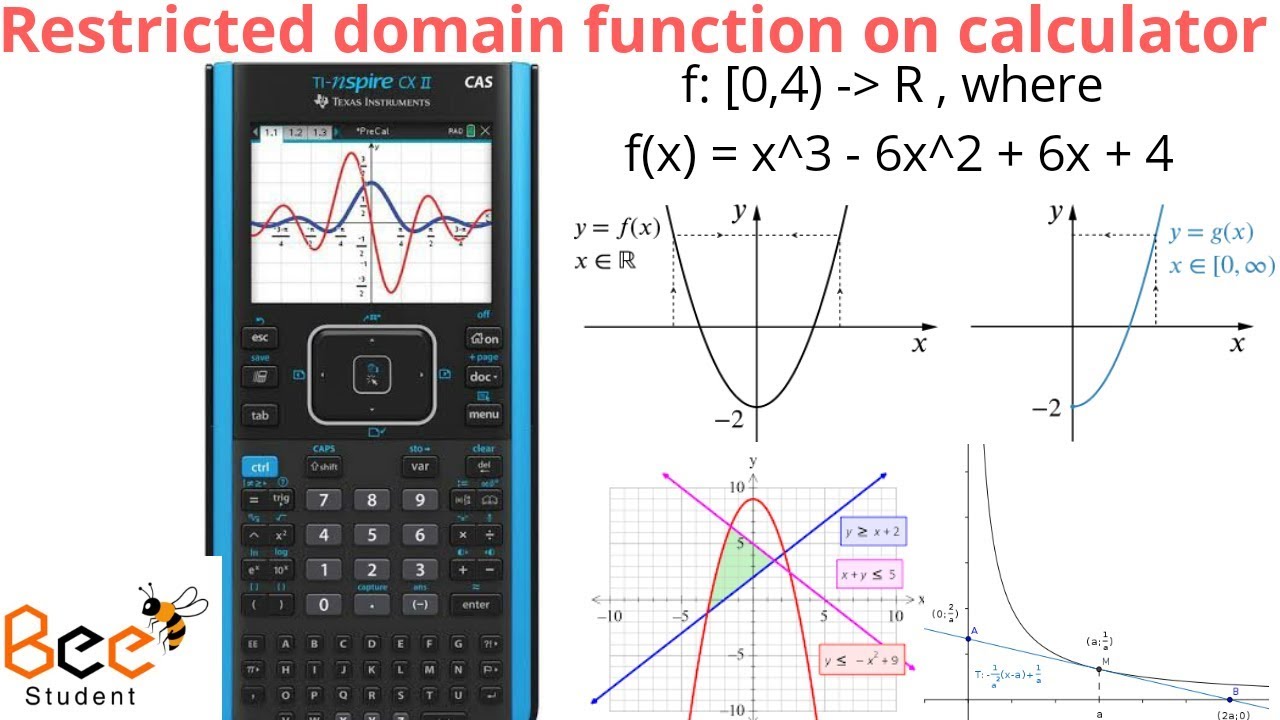
In either notation, you do exactly the same thing: you plug −1 in for x, multiply by the 2, and then add in the 3, simplifying to get a final value of +1.īut function notation gives you greater flexibility than using just " y" for every formula.
Evaluating piecewise functions calculator plus#
Now you say " f ( x) = 2 x + 3 find f (−1)" (pronounced as " f-of- x equals 2 x plus three find f-of-negative-one"). You used to say " y = 2 x + 3 solve for y when x = −1". Interactive online graphing calculator - graph functions, conics, and inequalities. For functions, the two notations mean the exact same thing, but " f ( x)" gives you more flexibility and more information. The evaluation of piecewise functions is done in the following way. The same is true of " y" and " f ( x)" (pronounced as "eff-of-eks"). Variables are more flexible, easier to read, and can give you more information. Hopefully you enjoyed that.In other words, they switched from boxes to variables because, while the boxes and the letters mean the exact same thing (namely, a slot waiting to be filled with a value), variables are better. Remind students that a piecewise function is not consistently defined by one equation so the first step when evaluating a piecewise function is always to determine which of the two or more equations applies. Type of function notation, it becomes a lot clearer why function notation is useful even. In our experience, piecewise functions can be challenging for students, mainly because of the notation. We have just constructed a piece by piece definition
Evaluating piecewise functions calculator how to#
Evaluate the function for the given value of x This section covers: Introduction to Piecewise Functions Evaluating Piecewise Functions Graphing Piecewise Functions How to Tell if a Piecewise Function is Continuous or Non-Continuous Obtaining Equations from Piecewise Function Graphs Absolute Value as a Piecewise Function Transformations of. The value of our function? Well you see, the value of Search: Evaluating Piecewise Functions Calculator. Worked example: evaluating piecewise functions. And x starts off with -1 less than x, because you have an openĬircle right over here and that's good because X equals -1 is defined up here, all the way to x is A piecewise function is a function built from pieces of different functions over different intervals. Give you the same values so that the function maps, from one input to the same output.
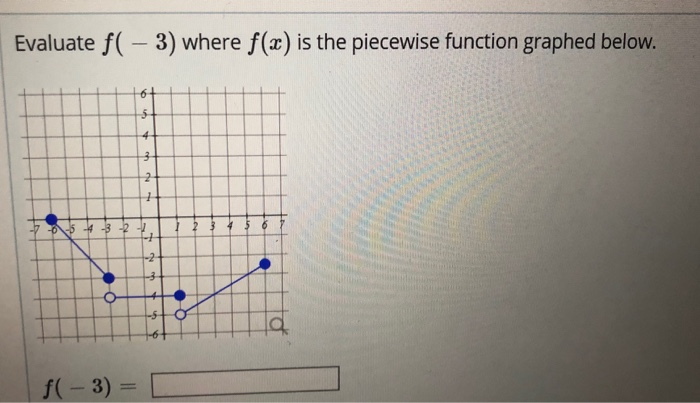
If you are in two of these intervals, the intervals should So it's very important that when you input - 5 in here, you know which

5 into the function, this thing would be filled in, and then the function wouldīe defined both places and that's not cool for a function, it wouldn't be a function anymore. Important that this isn't a -5 is less than or equal to. Here, that at x equals -5, for it to be defined only one place. Over that interval, theįunction is equal to, the function is a constant 6. The next interval isįrom -5 is less than x, which is less than or equal to -1. If it was less than orĮqual, then the function would have been defined at This says, -9 is less than x, not less than or equal. If t is between -10 and -2, we use this case. It's a little confusing because the value of the function is actually also the value of the lower bound on this Instructor Consider the following piecewise function and we say f (t) is equal to and they tell us what its equal to based on what t is, so if t is less than or equal to -10, we use this case.

Over this interval? Well we see, the value That's this interval, and what is the value of the function I could write that as -9 is less than x, less than or equal to -5. X being greater than -9 and all the way up to and including -5. Perform convolutions of continuous and discrete normal or piecewise functions. Is from, not including -9, and I have this open circle here. Different functions can be adapted to data with the calculator: linear. So let me give myself some space for the three different intervals. Then, let's see, our functionį(x) is going to be equal to, there's three different intervals. Over here is the x-axis and this is the y=f(x) axis. Let's think about how we would write this using our function notation. In this interval for x, and then it jumps back downįor this interval for x. A piecewise function is defined differently for different inputs and hence it has multiple pieces/shapes in its graph. This graph, you can see that the function is constant over this interval, 4x. View them as a piecewise, or these types of function definitions they might be called a Graphing calculator could be used to visualize the results of other computations (e. But what we're now going to explore is functions that areĭefined piece by piece over different intervals By now we're used to seeing functions defined like h(y)=y^2 or f(x)= to the square root of x.


 0 kommentar(er)
0 kommentar(er)
